
ESS210B
Prof. Jin-Yi Yu

Explained Variance for Multiple Regression
qAs an example, we discuss the case of two predictors for the multiple regression.
qWe can repeat the derivation we perform for the simple linear regression to find that the
fraction of variance explained by the 2-predictors regression (R) is:
here r is the correlation
coefficient
qWe can show that if r2y is smaller than or equal to a “minimum useful correlation” value, it is not useful to
include the second predictor in the regression.
qThe minimum useful correlation = r1y * r12
qThis is the minimum correlation of x2 with y that is required to improve the R2 given that x2 is correlated with x1.
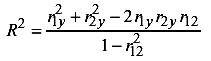

We want r2y > r1y * r12