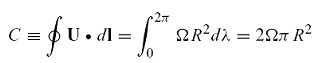ESS227
Prof. Jin-Yi Yu
Example
•In this case the circulation is just 2π times the
angular momentum of the fluid
ring about the axis of rotation. Alternatively, note that C/(πR2) = 2Ω so
that the circulation divided by the area enclosed by the loop is just twice the angular speed of rotation of the ring.
•Unlike angular momentum or angular velocity, circulation
can be computed without
reference to an axis of rotation; it can thus be used to characterize fluid rotation in situations where “angular velocity” is
not defined easily.
•That circulation is a measure of rotation
is demonstrated readily by considering a circular
ring of fluid of radius R in solid-body rotation at angular
velocity Ω
about the z axis.
•In this case, U = Ω × R, where R is the distance from the axis of rotation
to the ring of fluid. Thus the circulation
about the ring is given by: